
My research is currently supported by the NSF CAREER Award DMS-2142575. In the past, it was also supported by NSF Award DMS-1904342.
Papers and Talks
Publication list
Complete list of preprints and publications, in reverse chronological orderarXiv.org list
Complete list of submissions to the arXivORCID profile
List of publications hosted by ORCIDNotes and slides
Slides and handwritten notes from research talks, colloquia, and outreach talks.Research blurbs
My research can be broadly divided in two areas: Curvature and Topology, and Geometric Analysis.
An accessible overview of some aspects of my work in these fields is given below, emphasizing my interest in using ideas from both Pure and Applied Mathematics; see also this post on my NSF CAREER award.
Curvature and Topology

on average, positive curvature.
There are many remarkable ways in which the curvature of an object constrains its global shape (its "topology"), in the sense that it is impossible to deform some shapes so that they bend in certain ways.
For example, if a basketball is fully inflated, then it is round. In that configuration, it has constant positive curvature $K=1/r^2$, where $r$ is the radius of the ball. Once deflated, it can be deformed in many ways, which will change its curvature; however, the underlying shape, that is, the topology, never changes provided we do not cut into the plastic. But even if all the air is taken out, it is impossible to perfectly flatten this shape everywhere at once. Mathematically, an explanation is that the curvature $K$ of any sphere averages to a positive number, while the curvature of a flat surface, like a table top, is $K=0$. So one would find a contradiction if the sphere could be flattened: a positive number would be equal to zero. In slightly more precise terms, if a surface is obtained by smoothly deforming a sphere, then, at most points, it is locally on one side of the plane to which it is tangent. Here is a quick visual guide of what surfaces with curvature $K<0$, or $K=0$, or $K>0$ look like:
The above is an instance of the Gauss-Bonnet Theorem: the average curvature on any closed surface $M$ is a positive multiple of its Euler characteristic $\chi(M)$, a quantity only related to its topology; in symbols, $$\int_M K\,\mathrm{d}A = 2\pi\,\chi(M).$$ As the sphere has $\chi(M)=2$, no matter how it is deformed, it will, on average, still have positive curvature. This type of result is a topological obstruction: the topological condition $\chi(M)>0$ obstructs the geometric possibility that $K=0$ at all points of $M$. (Of course, it also obstructs $K\leq0$ at all points of $M$.) An even more remarkable fact is the following "recognition tool": if we do not know the shape of the closed surface $M$, but only know that it has $K>0$ everywhere, then we can use the above to find out it has $\chi(M)>0$. The classification of closed (orientable) surfaces then tells us the only possibility is that $M$ is a sphere!
Expanding our horizons, let us now consider higher-dimensional generalizations of surfaces, called Riemannian manifolds. These abstract geometric objects are intrinsically interesting in Mathematics, but are also important in many other contexts, from Robotics and General Relativity, to Data Science and Machine Learning. A natural way to measure curvature in a Riemannian manifold $M$ is to consider $2$-dimensional surfaces inside of them, whose curvature $K$ (in the sense above) is called the sectional curvature $\sec$ of the $2$-dimensional plane tangent to that surface. Just like surfaces, Riemannian manifolds also have an underlying topology, or global shape.
Lots of fundamental questions about interactions of curvature and topology on Riemannian manifolds remain unanswered. Some of the most famous examples of such open problems (also among my favorites) are the Hopf questions, the Bott conjecture (promoted by Grove and Halperin) that manifolds with $\sec\geq0$ ought to be rationally elliptic, the Stolz conjecture on Ricci curvature and the Witten genus, and the scarcity of examples of closed manifolds with $\sec>0$ in dimensions $\geq25$ other than spheres and projective spaces. Classical techniques have been mostly used to their exhaustion to attack these problems (in some cases, over many decades), so I focus on finding innovative approaches to shed some light on them.
Most of my work in this field (often with collaborators) aims to find novel ways of unpacking the geometric and topological information contained in the curvature operator $R\colon\wedge^2 TM\to\wedge^2 TM$, which is the most comprehensive notion of curvature on a Riemannian manifold $M$, from which any other type of curvature (sectional, Ricci, scalar, etc.) can be derived. This is a fairly complicated object; e.g., according to Gromov (p. 10), the curvature tensor of a Riemannian manifold is a little monster of (multi)linear algebra whose full geometric meaning remains obscure. In particular, my recent work often builds on the Finsler-Thorpe trick for curvature operators in dimension $4$, which is a characterization of sectional curvature bounds: $$\sec \geq 0 \quad \Longleftrightarrow \quad \exists\, \tau\in\mathbb R,\;\; R+\tau\, *\succeq 0,$$ where $*$ is the Hodge star operator. The above implies that the set of curvature operators with $\sec\geq 0$ in dimension $4$ is a spectrahedral shadow, opening the door to use semidefinite programming and other computational tools from Convex Algebraic Geometry to test whether $\sec\geq0$ is satisfied in an efficient way, and to optimize geometrically/topologically relevant functions on such curvature operators, such as the Chern-Gauss-Bonnet integrand, leading to bounds on $\chi(M)$. Although sectional curvature bounds in dimensions $\geq5$ do not give rise to spectrahedral shadows, inner and outer approximations can be used to derive bounds on curvature polynomials from Chern-Weil theory, thus on characteristic numbers of $M$. Related lines of research that I am pursuing involve using other geometric structures, such as twisted spinors, or symmetries, to seek topological obstructions to curvature conditions. An equally interesting (but very challenging) research direction is to construct new manifolds with $\sec>0$.
Geometric Analysis

In many situations, an energy can be associated to each possible state or geometric arrangement of an object, in a way that is often (but not always) motivated by physical considerations. One expects, by the Principle of Least Action, that the object will typically be found in a state that minimizes energy. These so-called ground states are stable stationary states since, after a small perturbation, the object naturally returns there. However, from a mathematical point of view, unstable stationary states are also very interesting, although (or, perhaps, because) they are harder to find in nature. Moreover, the transition from stable to unstable when a parameter is varied can often be used to detect the presence of other unstable solutions nearby, a phenomenon that Poincaré dubbed bifurcation, and which is extensively studied in Dynamical Systems.
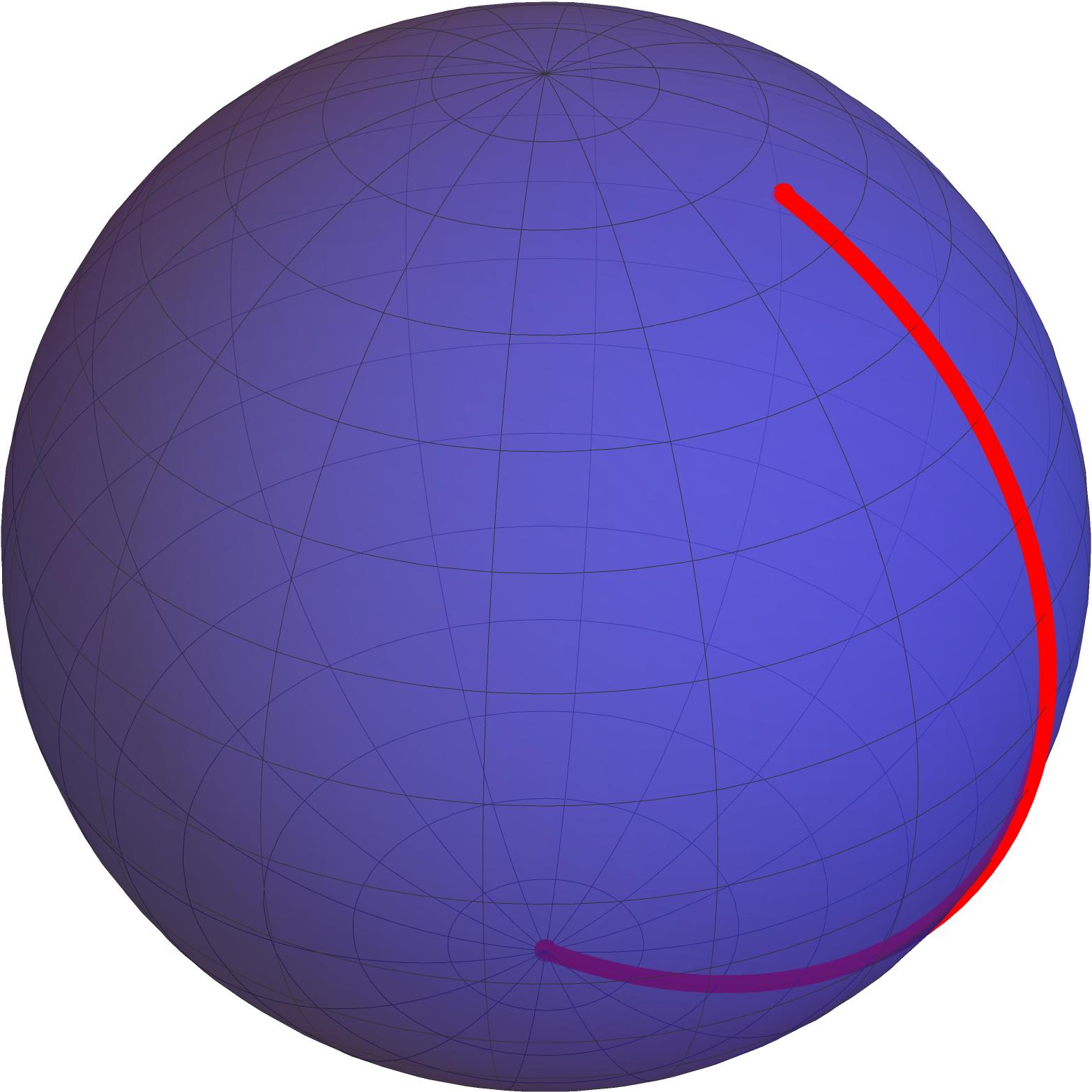
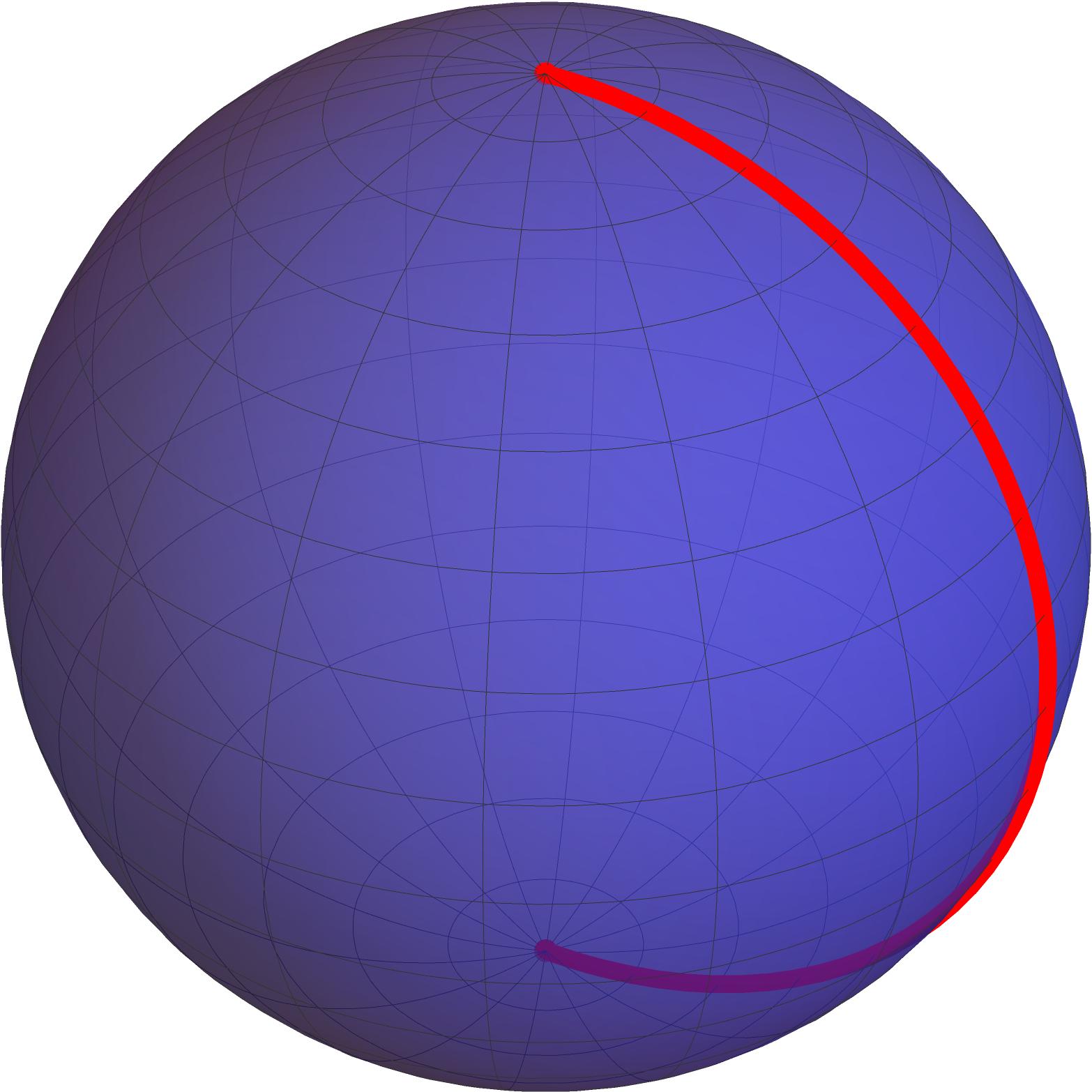
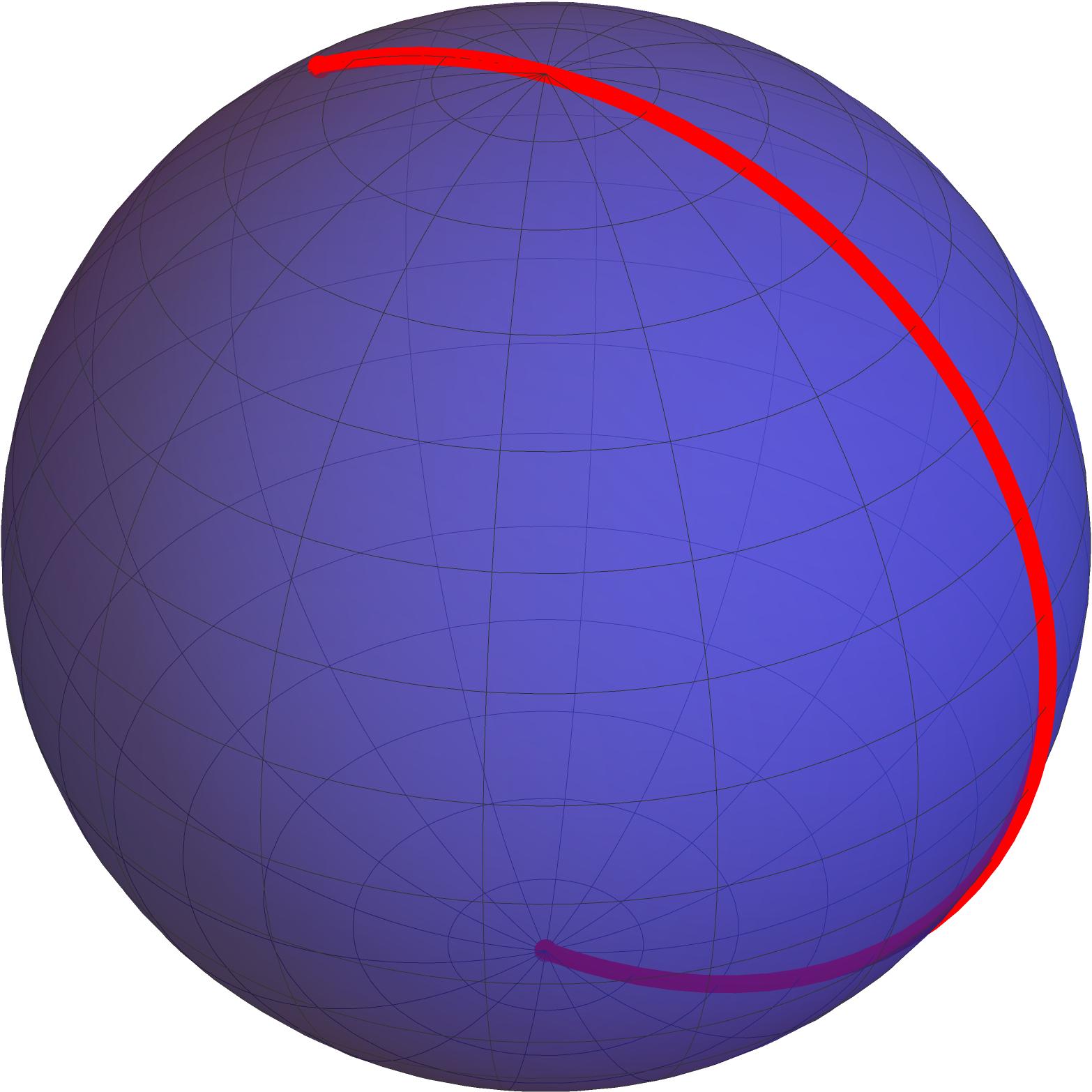
For example, imagine a spider that lives in a small spherical world and anchors its web at the South Pole, then starts moving towards the North Pole. The web wire is elastic and pulls tight instantly, without getting caught anywhere except for the endpoints, which are attached to the South Pole and to the spider itself, so it always traces a portion of a meridian on the sphere. Before the spider reaches the North Pole, the web wire is stable; indeed, it is the only curve on the sphere that minimizes distance between its endpoints. However, when the spider crosses the North Pole, there is a degeneracy instant and it goes from being stable to unstable: if the spider moves slightly off the meridian path, then the wire pulls tight and hence snaps to the "opposite" side of the sphere, where the distance to the South Pole is now shorter. This loss of stability captures the fact that there are multiple paths on the sphere minimizing distance from the South Pole to the North Pole.

Mathematically, these paths that (locally) minimize distance are called geodesics; physically, they can be used to represent light rays, and trajectories of free falling objects. In General Relativity, multiplicity of lightlike geodesics is closely related to gravitational lensing.

SMACS 0723 obtained by NASA's
James Webb Space Telescope,
displaying gravitational lensing.
In the example above, multiple geodesic segments are easy to spot directly. On the other hand, the existence of multiple solutions in more complicated situations is often established indirectly, without describing the solutions explicitly, following the strategy of detecting loss of stability along a "trivial" family of solutions, that we know exists a priori.
My research in this field (frequently with collaborators) implements this strategy to prove existence of multiple solutions to various problems in Geometric Analysis, such as the Yamabe problem and the problem of finding minimal surfaces, or, more generally, constant mean curvature surfaces. In particular, most of my recent work involves analyzing degenerations of highly symmetric solutions, from which less symmetric (thus harder to find) solutions sometimes bifurcate. While the above example of finding geodesics is encoded by an ordinary differential equation, these problems are usually encoded by nonlinear partial differential equations. In all cases, solutions to these equations are stationary points $x\in X$ of an energy functional $E_a\colon X\to\mathbb R$ that depends on a parameter $a\in\mathbb R$. This means they are zeros of its first variation, that is, solutions to the Euler-Lagrange equation $\delta E_a(x)=0$. Here, varying the parameter $a$ corresponds to varying the geometry of the problem; for instance, the endpoint of the geodesic (the position of the spider) in the example above. Furthermore, one assumes that, for all values of $a$, there is a solution $x_a$ to the problem, which is "trivial" in the sense that it is easy to find. The second variation $\delta^2 E_a$ is represented by a so-called Jacobi operator, which is typically a Schrödinger-type operator consisting of a Laplacian term and a curvature term. Solutions are stable if and only if all eigenvalues of this operator are nonnegative. Under certain structural hypotheses, solutions bifurcate from $x_a$ when the parameter crosses an instant $a=a_*$ at which an eigenvalue of the Jacobi operator changes sign; this means that, for $a$ near $a_*$, there are stationary points of $E_a$ different from $x_a$. These bifurcating solutions form a branch that may persist for values of $a$ far from $a_*$, and such global bifurcations lead to interesting nonuniqueness results. More details can be found in a Notices of the AMS survey article that I wrote with P. Piccione in 2020.
Some related lines of research that I am involved in consist of analyzing how rigid or malleable geometric configurations are under various intrinsic or extrinsic conditions and deformations (for example, rank rigidity phenomena), qualitative behavior of solutions to geometric evolution equations, such as Ricci flow and Mean Curvature Flow, and spectral geometry of highly symmetric objects, such as homogeneous spaces.