Teaching Mathematical Physics

Mathematical Physics PHY 307 -- Fall 2010

Material covered:

(Syllabus)

Week	Tuesday	Thursday
Aug 23		First day of classes: General Introduction
Aug 30	Plotting and Animation Vectors and Lists	Derivatives and Series
Sep 06	Labor Day	Partial derivatives and vector calculus
Sep 13	No class	Vector calculus (continued)
Sep 20	Sums, Series, Products	Integrals
Sep 27	Multiple integrals	Multiple integrals (continued)
Oct 04	Contour and surface integrals	Contour and surface integrals (continued)
Oct 11	Equations and systems of equations	Discussion of the homework and other problems
Oct 18	Ordinary differential equations (ODE), classification	ODE, analytical methods of solution
Oct 25	ODE: pendulum, viscous friction	ODE with more complicated boundary conditions; shooting
Nov 01	Linear ODE with constant coefficients. Complex numbers	Numerical solution of ODE
Nov 08	Numerical solution of systems of many ODEs: Molecular dynamics	Stability of ODE. Pendulum and thermal runaway
Nov 15	Home work survey	Partial differential equations. Classification and physical examples
Nov 22	PDE. Wave equation in fluids	Thanksgiving
Nov 29	PDE. Heat conduction equations	PDE. Schrödinger equation
Dec 6	Eigenvalue problems	Eigenvalue problems

Problem sets:

Aug 30	Sep 06	Sep 13	Sep 20	Sep 27	Oct 04

Recommended books

       This course is an original course that can be titled "Essentials of Mathematical Physics with Numerical Methods based on Wolfram Mathematica". We consider practical solutions, analytical and numerical, of basic physical problems, as well as of mathematical problems related to physics. Care is taken to keep the course as simpe as possible. For this reason some more complicated analytical material inherent in Mathematical Physics is omitted in favor of numerical solutions.
       Multidisciplinary character of this course and extensive use of technology make the learning curve steeper. Yet, in our age learning Mathematical Physics without a possibility to immediately see the solution of a practical problem on computer's screen is hardly justified. This course will give students majoring in physics a practical tool for their research.
        Although a prerequisite for this course is upper-undergraduate skills in physics and mathematics, the course is built in a self-consistent way so that most of the concepts are explained here, although briefly.

Topics:

Data visualization. Plots and animations
Vectors and matrices
Derivatives
Series expansions
Vector calculus
Series
Integrals
Equations
Complex numbers and functions
Ordinary differential equations and systems of equations
Molecular dynamics
Partial differential equations
Eigenvalue problems
Delta functions
Fourier transformation and Fourier series
Applications of Fourier series
Minimization and maximization
Interpolation and fitting
Special functions

Official description of the course from Lehman web site

PHY 307: Mathematical Physics.

4 hours, 4 credits. Vector calculus, matrix and tensor algebra, Fourier and Laplace transforms, complex variable theory, and solutions of differential equations. Applications to problems in physics. PREREQ: Either PHY 167 or 169. PRE- or COREQ: MAT 226.

Examples of what we can do:

One-slit diffraction of a wave

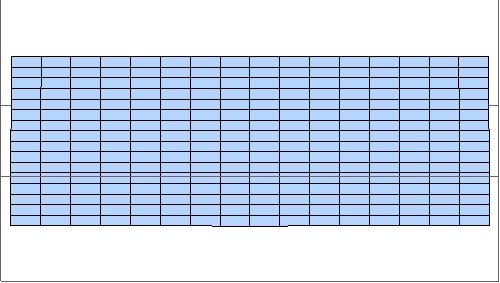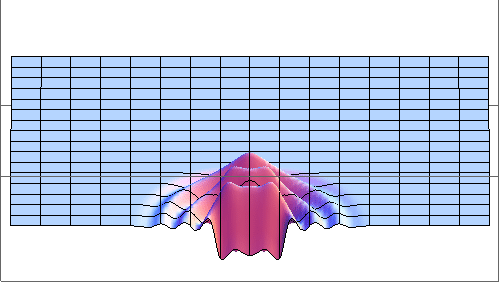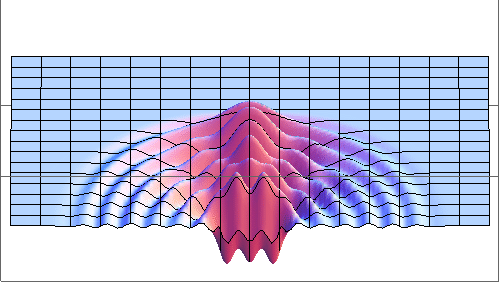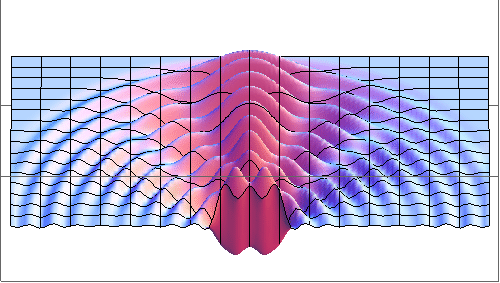
Time-dependent wave equation has been solved by Wolfram Mathematica.
One can see diffraction minima at the directions q specified by

d sinq = ml, m = ±1, ±2,...

Here d is the width of the slit and l is the wave length. The process has been stopped before the wave front hits the far wall to avoid reflections that create a mess.

One-slit diffraction of a quantum particle

Time-dependent Schrödinger equation is solved by Wolfram Mathematica and the probability density |Y|² is plotted. One can see diffraction minima at the directions q specified by

d sinq = ml, m = ±1, ±2,...

similarly to the diffraction of the wave above (parameters are the same). Reflection of the particle from the far wall leads to interference between the incident and reflected waves and steady increase of the total probability since particles steadily enter the region via the slit.

This fractal has been obtained by simple mathematical transformations (100 millions of iterations) with the help of Mathematica.

Another example of using Mathematica is my animation "Wheel rolling on a plane" made for the course of Classical Mechanics at the Graduate Center (the bottom of the page)